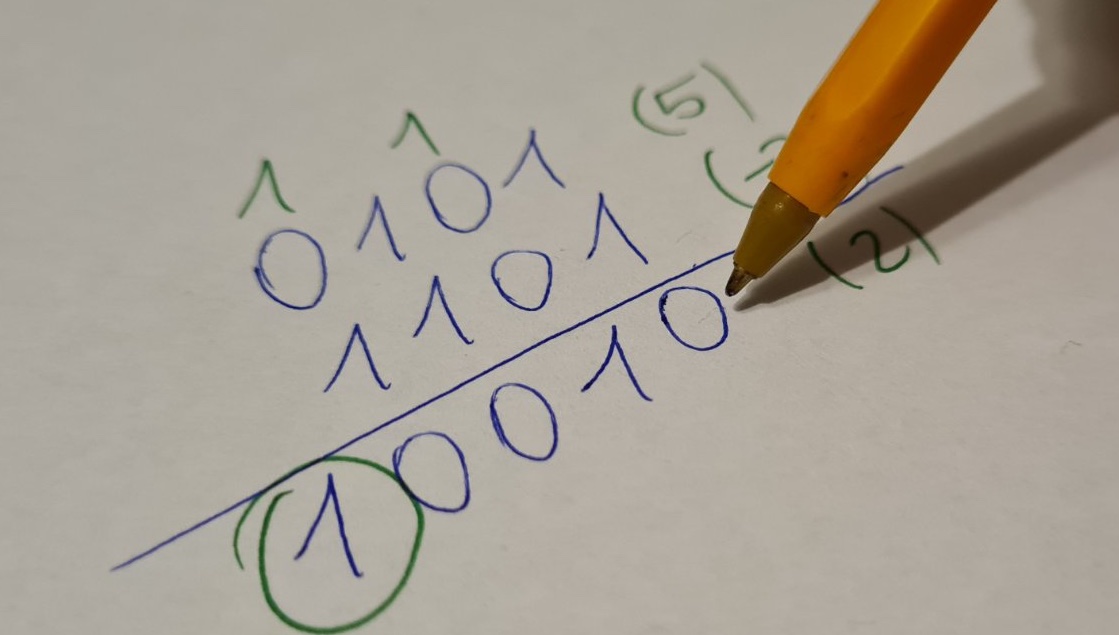
Introduction

In most modern programming languages, there are signed and unsigned numeric types, e.g. unsigned int in C++ or uint in C#. Java did not introduce unsigned types! The most probable reason is to make Java simple. What if we really need to use an unsigned integer or unsigned long? There is a workaround that I will explain in this article. Before we do it, let’s understand how integer numbers are represented internally.

Motivation

For many years of development in Java, I rarely had the need to use unsigned integers, from a technical point of view. If we lose 1 bit from 32, it is not a big deal. If the Integer is too small, we can use Long with Long.MAX_VALUE is equal to nine quintillions (9223372036854775807). When Long type is not enough, we can still use BigInteger with theoretical unlimited size.

I would divide a need of having unsigned integer type into two cases:

make a logical representation of items, for example, to represent a number of wheels on the car. For most cases, unsigned integer is a perfect choice. What would it mean that the car has -2 wheels? In fact, we use a signed integer for it. Whereas, I would like to avoid a philosophical discussion if we need unsigned integers to properly represent our models.
technical aspects.

I find it useful to have unsigned integers in 2 areas:

when we make low-level operations, e.g. integration with electronic devices. This also means that it is impossible to directly exchange numeric data between C and Java programs.
Cryptography also relies on such types to some extent; this makes it more difficult to write applications that use cryptography in Java,
when we need really high performant operations on unsigned integer (memory and speed) during mathematical calculations. This was my initial motivation to investigate the topic.

I believe that you as a Reader can find more cases where an unsigned integer is required.

Binary format

As we know, the computer uses a binary format to represent numbers. Each position represents a power of two.

01 = 0² + 1¹ = 1
10 = 1² + 0¹ = 2
11 = 1² + 1¹ = 3

The binary format in Java

Java uses two’s complement to store integers.

Signed positive numbers

Let’s consider how Java stores positive signed numbers. For simplicity, let’s say that we have 4 bits numbers. The first bit determines the sign. 0 means that the number is positive. To represent the actual value of the number, we have 3 other bits. Examples:

0011 = 0 on the left means that the number is positive
011 value is equal to: 0² + 2¹ + 2⁰ = 3

0101 = 0 on the left means that the number is positive
101value is equal to: 2² + 0¹ + 2⁰ = 5

Negative numbers

Negative numbers are much more complicated to represent. Java uses two’s complement representation. The movie below explains how one’s complement and two’s complement representation works.

To summarize:

The negative numbers are represented by inverting 1's to 0's and vice versa for all of the bits in a value, then adding 1 to the result.

For example: let’s build -5 from 5 number:

0101 = 5
1010 (inverted values)
1011 (added 1 to inverted values) = -5

For 4 bits, all the numbers represented in two’s complement form look like:

= -8
= -7
= -6
= -5
= -4
= -3
= -2
= -1
=  0
=  1
=  2
=  3
=  4
=  5
=  6
=  7

What is worth mentioning:

we have values from -8 to +7, (accordingly: Integer.MAX_VALUE = 2_147_483_647, Integer.MIN_VALUE = -2_147_483_648) - there is one more negative value than positive.
in contrast to ones’ complement representation, we have only one zero value.

Adding numbers

One of the biggest advantages of having two’s complement form is the easy way of adding numbers. It works in the same way as the algorithm learned at school. Let’s follow the example for 4 bits number:

   1 1   (carry-over)
   0101  (5) 
   1101 (-3)
------------
[1]0010  (2)

The result here is 10010. The carry-over made this number 5 bits long. We drop the first bit to make it 4 bits long. The result is 0010 as binary, equal to 2 in decimal form.

Overflow

Java doesn’t do anything with integer overflow for either int or long primitive types and ignores overflow with positive and negative integers. Example:

If we add 1 to the maximal integer value, we will simply overflow to the integer min value.

 01111111111111111111111111111111 = 2_147_483_647 = Integer.MAX_VALUE
+00000000000000000000000000000001 = 1
---------------------------------
 10000000000000000000000000000000 = -2147483648 = Integer.MIN_VALUE

If we subtract 1 from the minimal integer value (in the example add -1) we will simply overflow to integer max value.

 10000000000000000000000000000000 = -2_147_483_648 = Integer.MIN_VALUE
+11111111111111111111111111111111 = -1 
---------------------------------
 01111111111111111111111111111111 = 2_147_483_647 = Integer.MAX_VALUE

JVM will not throw an exception, it will simply execute the operation.

Unsigned operations

Since Java 8, there are static helper methods for Long, Integer, Short, and Byte.

Conversion unsigned integers

To convert unsigned number from string to int type, we can use: Integer.parseUnsignedInt("4000000000", 10);. It will convert the number 4 billion (that cannot fit into 31 bits), with radix 10. Internally it will be signed decimal -294967296, but unsigned: 4000000000. Method Integer.toUnsignedString(value) converts binary representation to string and treats it as an unsigned integer.

Let’s analyze the code below:

int value = Integer.parseUnsignedInt("4000000000", 10);
System.out.println("decimal value = " + value);
System.out.println("binary representation = " + Integer.toUnsignedString(value, 2));
System.out.println("unsigned decimal representation = " + Integer.toUnsignedString(value));

output:

decimal value = -294967296
binary representation = 11101110011010110010100000000000
unsigned decimal representation = 4000000000

Adding unsigned integers

Let’s see if we can add two integer numbers and cross Integer.MAX_VALUE = 2_147_483_647.

int value = Integer.parseUnsignedInt("2000000000");
value = value + value;
System.out.println("decimal value = " + value);
System.out.println("binary representation = " + Integer.toUnsignedString(value, 2));
System.out.println("unsigned decimal representation = " + Integer.toUnsignedString(value));

output:

decimal value = -294967296
binary representation = 11101110011010110010100000000000
unsigned decimal representation = 4000000000

The value 2000000000 (2 billion) almost exceeds the Integer.MAX_VALUE. If we double this value, the result will still be in 32 bits, but the integer with a sign cannot handle it. It will overflow. That’s why we see decimal result -294967296. Whereas in the unsigned format it is 4000000000.

Multiplying unsigned integers

Multiplication works in the same way. Instead of adding 2 billion to each other, I multiply it by 2.

int value = 2_000_000_000;;
value = value * 2;
System.out.println("decimal value = " + value);
System.out.println("binary representation = " + Integer.toUnsignedString(value, 2));
System.out.println("unsigned decimal representation = " + Integer.toUnsignedString(value));

output:

decimal value = -294967296
binary representation = 11101110011010110010100000000000
unsigned decimal representation = 4000000000

In the case of multiplying, the result looks the same as for adding. In decimal format we see overflow (-294967296), but in the unsigned decimal representation we see a proper result (4000000000).

Division unsigned integers

The division is also possible with unsigned integers. JDK introduced method: Integer.divideUnsigned(int dividend, int divisor).

int value = Integer.parseUnsignedInt("4000000000");
value = Integer.divideUnsigned(value, 2);
System.out.println("decimal value = " + value);
System.out.println("binary representation = " + Integer.toUnsignedString(value, 2));
System.out.println("unsigned decimal representation = " + Integer.toUnsignedString(value));

output:

decimal value = 2000000000
binary representation = 1110111001101011001010000000000
unsigned decimal representation = 2000000000

In this example, we were able to divide 4 billion by 2 in the correct way.

Alternative solutions

If we do not want to use JDK, Guava library provides UnsignedInts a wrapper class.

UnsignedInteger value = UnsignedInteger.valueOf(2_000_000_000);
value = value.times(UnsignedInteger.valueOf(2));
System.out.println(value);

output:

4000000000

Summary

Officially Java didn’t introduce unsigned integer types. Whereas the workaround was introduced in Java 8 and a determined developer can make these operations if really required.

Marek Hudyma's Engineering Blog

Java unsigned integer

Introduction

Motivation

Binary format

The binary format in Java

Signed positive numbers

Negative numbers

Adding numbers

Overflow

Unsigned operations

Conversion unsigned integers

Adding unsigned integers

Multiplying unsigned integers

Division unsigned integers

Alternative solutions

Summary

Marek Hudyma